Articles
- Page Path
- HOME > Osong Public Health Res Perspect > Volume 12(4); 2021 > Article
-
Review Article
COVID-19 prediction models: a systematic literature review -
Sheikh Muzaffar Shakeel
 , Nithya Sathya Kumar
, Nithya Sathya Kumar , Pranita Pandurang Madalli
, Pranita Pandurang Madalli , Rashmi Srinivasaiah
, Rashmi Srinivasaiah , Devappa Renuka Swamy
, Devappa Renuka Swamy
-
Osong Public Health and Research Perspectives 2021;12(4):215-229.
DOI: https://doi.org/10.24171/j.phrp.2021.0100
Published online: August 13, 2021
Department of Industrial Engineering and Management, JSS Academy of Technical Education, Bengaluru, India
- Corresponding author: Sheikh Muzaffar Shakeel Department of Industrial Engineering and Management, JSS Academy of Technical Education, JSSATE-B Campus, Dr. Vishnuvardhan Rd Uttarahalli-Kengeri Main Road, Post, Srinivaspura, Bengaluru, Karnataka 560060, India E-mail: shaikhmuzzu99@gmail.com
- Co-Corresponding author: Nithya Sathya Kumar Department of Industrial Engineering and Management, JSS Academy of Technical Education, JSSATE-B Campus, Dr. Vishnuvardhan Rd Uttarahalli-Kengeri Main Road, Post, Srinivaspura, Bengaluru, Karnataka 560060, India E-mail: nithyask19@gmail.com
© 2021 Korea Disease Control and Prevention Agency
This is an open access article under the CC BY-NC-ND license (http://creativecommons.org/licenses/by-nc-nd/4.0/).
Abstract
- As the world grapples with the problem of the coronavirus disease 2019 (COVID-19) pandemic and its devastating effects, scientific groups are working towards solutions to mitigate the effects of the virus. This paper aimed to collate information on COVID-19 prediction models. A systematic literature review is reported, based on a manual search of 1,196 papers published from January to December 2020. Various databases such as Google Scholar, Web of Science, and Scopus were searched. The search strategy was formulated and refined in terms of subject keywords, geographical purview, and time period according to a predefined protocol. Visualizations were created to present the data trends according to different parameters. The results of this systematic literature review show that the study findings are critically relevant for both healthcare managers and prediction model developers. Healthcare managers can choose the best prediction model output for their organization or process management. Meanwhile, prediction model developers and managers can identify the lacunae in their models and improve their data-driven approaches.
- Healthcare refers to the organized provision of medical care to people and communities. It constitutes the efforts made by qualified and licensed practitioners to preserve or achieve physical, mental, or emotional well-being. Healthcare and medical facilities are regarded as making a significant contribution to the promotion of individuals’ health and well-being. The healthcare industry is responsible for manufacturing and distributing the drugs and services needed to safeguard, cure and sustain well-being. Providing healthcare for patients affected by coronavirus disease 2019 (COVID-19) has been challenging, especially in India and in Karnataka in particular. Several studies have been performed to understand the spread of COVID-19 and to deal efficiently with COVID-19 patients. The motivation of this study was to collate the available information on various prediction models and to choose accurate models for anticipating the number of cases. Many governments have collected and are trying to analyze data to be better equipped for providing healthcare to COVID-19 patients. The COVID-19 pandemic challenged healthcare facilities, with the sheer number of cases resulting in an acute shortage of capacity that constrained healthcare services [1]. A study was conducted to identify the best social media platform that can be employed for sentiment analysis and data mining, and the reported methods of data extraction and methodological consideration provide a basis for planning future studies [2]. State-of-the-art techniques for COVID-19 prediction algorithms are based on commonly used data mining and machine learning techniques to benefit the healthcare sector [3]. The management of the healthcare system focuses on the overall governance of public health services, including the appropriate and effective use of clinical infrastructure facilities, with a view to attaining the highest benefits for human health.
- With the worldwide spread of the COVID-19 pandemic, which causes potentially severe respiratory illness, healthcare systems are facing challenges in order to provide appropriate treatment to support patients. In accordance with the goals of healthcare, there are several factors and aspects of the medical sector that must be actively planned and organized.
- Adopting a multi-criteria decision framework, such as the Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS) method, is an effective approach to prioritize COVID-19 patients that facilitates detection of the health conditions of asymptomatic carriers and helps stakeholders tackle the complex problem of COVID-19 [4–6]. The TOPSIS framework was developed based on machine learning and multiple-criteria decision-making via the subjective and objective decision by opinion score method to provide effective care and prevent the extremely rapid spread of COVID-19 from affecting patients and the medical sector [3].
- Based on the findings of the systematic literature review (SLR), it is recommended that healthcare systems and stakeholders should use the best prediction model to forecast the number of cases and make the necessary arrangements for imposing social distancing and lock-down measures during the pandemic.
- The present study provides insight into various prediction models and how to choose the best model in terms of maximizing accuracy and minimizing errors. This information will be vital in decision-making for government, the healthcare sector and other stakeholders. The findings of this study have implications for the quality of healthcare management. The health system is expected to perform well in all aspects of satisfying the needs of the customers whether those customers are patients, attending physicians, employers, or functional departments within an organization. The current study presents an SLR of papers published from January 2020 to December 2020. The study applied a specific set of inclusion and exclusion criteria to generate comprehensive tables reviewing the literature that contain information about various COVID-19 prediction models, the characteristics considered in prediction, sample size, and model accuracy.
- Spread of COVID-19 (World-wide Scenario)
- Pandemics are caused by pathogenic microorganisms (e.g., bacteria, viruses, parasites, and fungi) that tear through populations. The bubonic plague of the 14th century infected over 50 million people in Europe and the Spanish flu of 1918 infected a fifth of the world's population. Pandemic influenza, also termed H1N1 influenza/novel influenza/’swine flu,’ ravaged populations worldwide in more recent years [7].
- COVID-19 is an infectious disease that affects the human respiratory system. In December 2019, the illness was first reported in Wuhan, the capital of China’s Hubei province. At the end of December 2019, a number of patients were admitted to hospitals with an initial pneumonia diagnostic test showing an unknown etiology. Since then, COVID-19 has spread around the globe. At the time of writing this paper (July 26, 2021), 90,698,044 cases of the virus had been recorded worldwide. COVID-19 was formally declared a global pandemic on March 11, 2020 by the World Health Organization (WHO). The top countries affected by COVID-19 are classified in terms of cases reported, deaths, and recovered cases (Table 1). The United States of America (USA), India, Brazil, Russia, France, United Kingdom, Turkey, Argentina, Colombia, and Spain are the top 10 countries affected by COVID-19. On January 13, 2020, the first case outside China was identified in Thailand [8,9]. The first case of COVID-19 was reported in the USA on January 23, 2020 [10].
- Spread of COVID-19 in the Indian Context
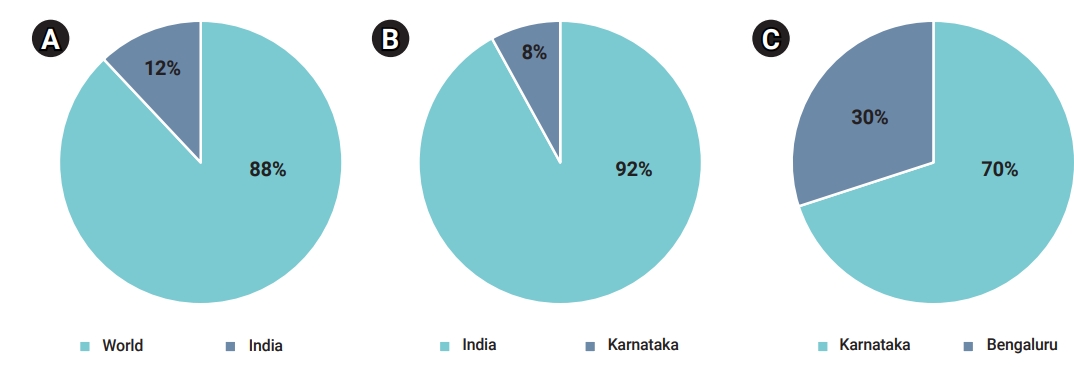
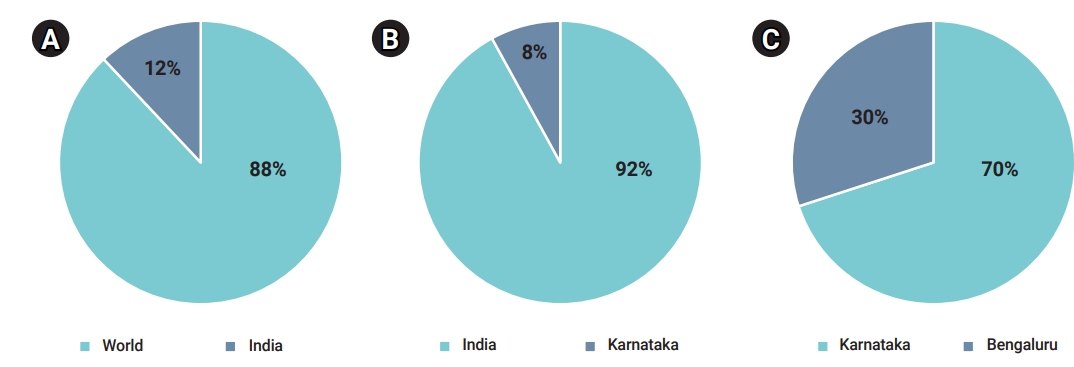
- India, which is the second most populated country after China, is the country in South Asia with the most COVID-19 cases. On January 30, 2020, India recorded the first case of the disease. Since then, cases have increased significantly and dramatically. In order to reduce the transmission of COVID-19, the government of India announced a nationwide lock-down starting on March 25, 2020, which continued for about 2 months. The number of COVID-19 cases as of July 31, 2021 has reached 197,548,856 confirmed cases and 4,213,071 cases. Within India, Karnataka is the second most strongly affected territory. In the early stages of the global pandemic, Karnataka registered fewer cases than most other Indian states. It was among the early states to deploy new equipment and tools as part of its infrastructure and containment initiatives. The first case in Karnataka was reported on March 9, 2020. The number of COVID-19 cases reported in Karnataka is 928,792 confirmed cases, 906,593 recovered cases and 12,142 deaths (as of January 11, 2021). The government of Karnataka incorporated a gradual lock-down, closing shops and offices, and shutting down inter-district and interstate journeys as part of the initiative to contain the outbreak. The period from March 24 to April 14, 2020 was phase 1 of the lock-down, with the strict restrictions on travel and social interaction. The second phase was from April 15 to May 3, and the third phase lasted from May 4 to May 17 [11]. Bengaluru, the capital of Karnataka, had more infections than other parts of the state. On March 9, 2020, the first COVID-19 case was identified in Bengaluru. As of January 11, 2021, the number of COVID-19 infections in Bengaluru amounted to 392,581 confirmed cases, 382,166 recovered cases, and 4,347 deaths. In terms of controlling the virus, Bengaluru has implemented various curfews, public awareness campaigns, and rigorous reverse-transcription polymerase chain reaction tests. The mapping of containment zones and predictive modeling conducted by Bruhat Bengaluru Mahanagara Palike (a local body) were vital factors for successfully controlling the pandemic (Figure 1).
- COVID-19 is primarily transmitted by close contact with the droplets spread by sneezing, coughing, and talking to an infected person [12]. The initial stages in COVID-19 transmission have been attributed to human exposure in the wet animal market in Wuhan, where live animals are frequently sold, and it is speculated that this wet market was likely the main source of COVID-19 [13]. Efforts are being made to search for transitional carriers from which the infection might have spread to humans; however, regardless of the original source, COVID-19 has shown an unprecedented degree of horizontal spread. Person-to-person transmission takes place by close contact or through droplets spread by an infected person’s cough or sneeze [14].
- WHO Definitions of Key Parameters
- Confirmed case: A person with laboratory confirmation of COVID-19 infection, irrespective of clinical signs and symptoms.
- Positive case (same as confirmed case): A person with laboratory confirmation of COVID-19.
- Active cases: The value obtained by subtracting the number of recovered cases and the number of deaths from total number of positive cases.
- Recovered cases: Those cured of COVID-19 and discharged from a healthcare facility, also referred to as “discharged.”
- Death: For surveillance purposes, a COVID-19 death is characterized as a death resulting from a clinically compatible disease in a likely or confirmed case of COVID-19, unless there is a specific alternative cause of death that cannot be attributed to COVID-19 (e.g., trauma). There should be no time of full healing between sickness and death.
- Symptoms: A moderate case is defined a confirmed case with fever, respiratory symptoms and radiographic evidence of pneumonia, whereas a case involving dyspnea or respiratory failure is defined as a severe case
- Objectives
- Owing to the wide spread of COVID-19 and its devastating effects on humans, several research groups have investigated various aspects of the virus, such as its epidemiological characteristics, socio-economic effects, and factors and parameters aiding the spread of the virus. The present work is an SLR with the following objectives: (1) To systematically review the prediction models that have been developed for COVID-19; (2) To analyze the various COVID-19 prediction models that are currently available; (3) To synthesize and extract useful results and conclusions about the COVID-19 prediction models.
- Methods
- An SLR is a supplementary methodology used to help evaluate studies by capturing principal analyses on the basis of specific criteria. An SLR is carried out on the basis of previous similar studies through a systematic review. The purpose of an SLR is to summarize the studies carried out and to identify gaps between previous studies and current studies.
- Okoli [15] stated that an SLR is “a systematic, explicit, detailed and repeatable approach to identify, assess and analyze the existing body of work by researchers, scholars and practitioners.” According to Tranfield et al. [16], an SLR is considered as a “fundamental scientific activity.” Moher et al. [17] presented a checklist for Preferred Reporting Items for Systematic Reviews and Meta-Analyses (PRISMA). The objective of this SLR was to understand further the mechanisms and analyses used in prediction models for COVID-19 infections. The research time period for this study was from December 2020 to January 2021. This study was conducted in 4 phases: (1) the development of literature search strategies, (2) the formulation of inclusion and exclusion criteria, (3) quality assessment, and (4) analysis and conclusion.
- Research Questions
- The wide spread of the COVID-19 pandemic has resulted in illness and loss of life on a global scale. Research teams have worked on various models to understand the spread of the virus and make data-driven predictions. For the purpose of this SLR, we articulated a research question (RQ) to help focus on the main issue. The motivation and RQs of this study were as follows:
- Motivation: To identify methods, techniques, models that support the prediction of COVID-19 infections.
- RQ1: What factors support the prediction of COVID-19 infections?
- RQ2: What methods and techniques are followed in data-driven modeling for predicting COVID-19 infections?
- Inclusion and Exclusion Criteria
- Current search engines provide a high level of recall, which leads to a large number of irrelevant resources being retrieved. Therefore, for effective results, a researcher must follow a systematic search strategy. This stage of an SLR screens the literature to find the relevant literature on the basis of particular criteria. In this study, 3 inclusion and exclusion criteria for identifying relevant content and restricting irrelevant content were adopted. The first inclusion criterion was the type of document: only published documents were included, whereas manuscripts under review and unpublished manuscripts were excluded. The domain (i.e., the subject area identified for the study) was the second screening criterion; the authors included documents containing prediction models developed for or used in the COVID-19 domain, while other documents were excluded. The last screening criterion was the language in which the document was released. In order to avoid confusion and complexity related to translation, only documents available in English were included, while documents in other languages were excluded (Table 2).
- Databases and Search Strategies
- The terms were searched in several databases (Google Scholar, Scopus, Publish or Perish, and Web of Science [WoS]). The search terms are as follows: prediction models, COVID-19, Coronavirus, SARS-CoV, SARS-CoV-2, healthcare, healthcare system, survival model, medical care. Various combinations of the search terms were used to retrieve resources in particular databases. Some of the search strings used are as follows—“Prediction models” AND “COVID-19”; “COVID-19 Datasets” AND “Prediction modeling”; “Predictive Analysis” AND “COVID-19 data” OR “Predictive Analysis” AND “Corona Virus”.
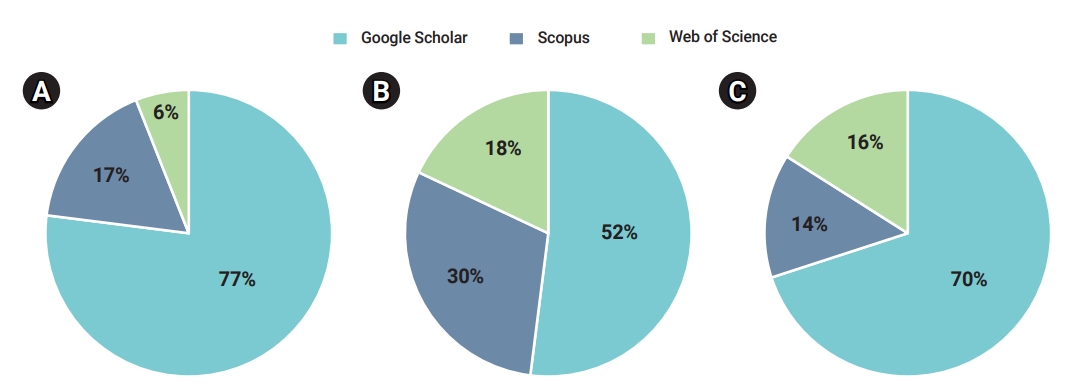
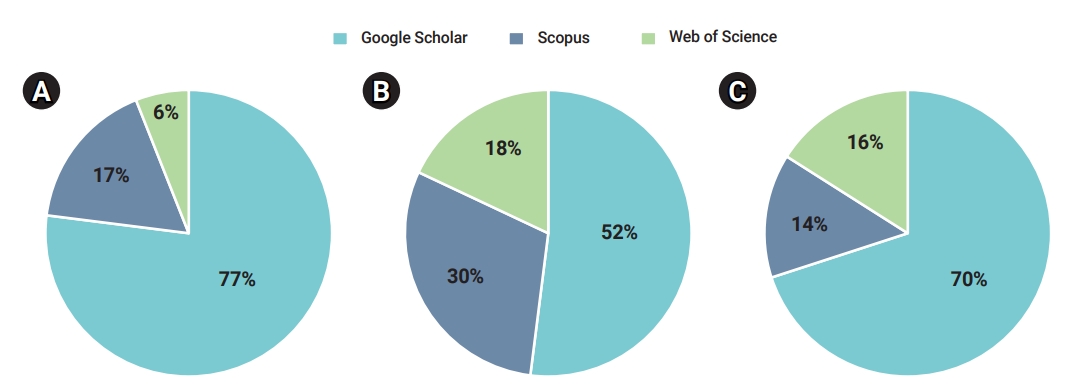
- After applying the inclusion and exclusion criteria, 1,196 documents were retrieved, of which 47 were duplicates. Therefore, a total of 1,149 documents continued to the second stage of scrutiny and quality assessment (Table 3). The percentage shares of articles from various databases in the initial, screening, and acceptance stages of the document selection process are illustrated.
- In the initial phase, out of the total number (i.e., 1,196 documents) of retrieved documents, Google Scholar accounted for 77%, Scopus contained 17%, and WoS had 6% (Figure 2A). After the initial screening, 62 documents were included for further consideration. During the screening phase, 52% of the initially included documents were retrieved from Google Scholar. Out of the remaining 30%, Scopus and WoS had an 18% share each (Figure 2B). Out of the total accepted documents, 70% were retrieved from Google Scholar, 14% from Scopus, and 16% from WoS (Figure 2C).
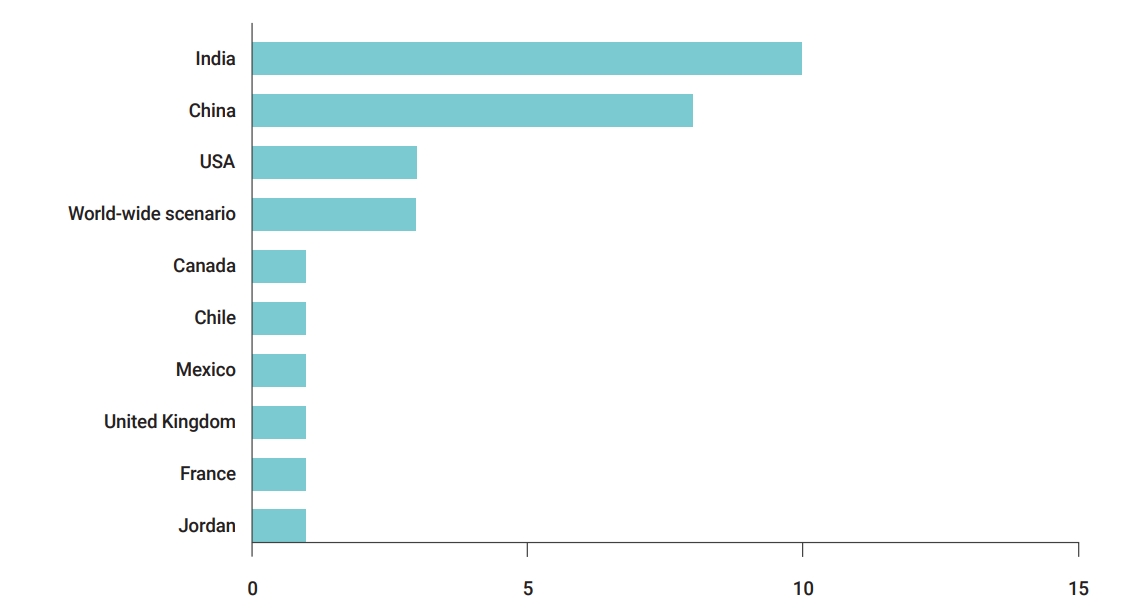
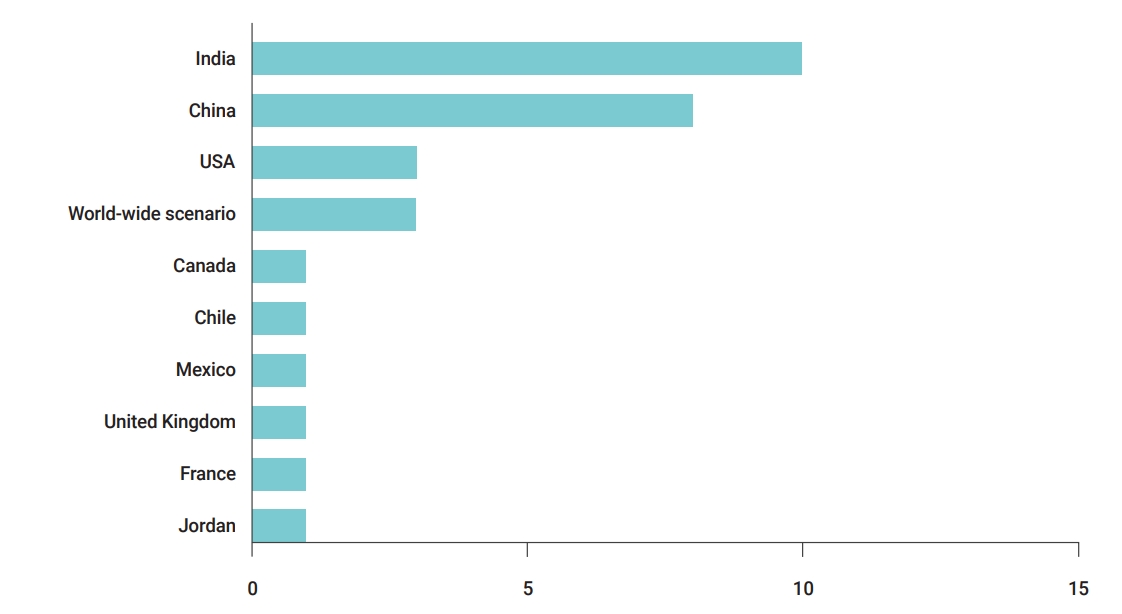
- The present study focused on publications dealing with COVID-19 prediction models across the world. This review was conducted in January 2021. The country of a research/case was defined by the affiliations of authors in the paper, and a limited research level was observed for several countries (e.g., Canada, Chile, France, Jordan, etc.). Given our particular focus on the spread of the pandemic in India, the highest number of publications was from India and China (Figure 3).
- Quality Assessment and Coding
- Quality evaluation of a phenomenon is conducted as a systematic way to avoid biases and errors. Thereby, an SLR includes quality assessment as an essential step. In this study, in the initial phase, 1,196 documents were chosen. Based on their titles, these documents were further analyzed and 62 documents were screened. The content was scrutinized on the basis of the title, abstract, introduction, and conclusion and 30 studies were finally selected for the review.
Introduction
- Prediction Models
- A prediction model is a method of becoming aware of a future scenario beforehand based on available data. Predictive modeling mainly uses statistics to predict outcomes [18]. Forecasting in the COVID-19 pandemic allows medical professionals to better manage facilities and to validate the use of medical and financial resources. It is essential to systematically assess the predictive outcomes of 1 or more prediction models in order to analyze the prediction accuracy of a framework across different study populations, ecosystems, and locations and to assess the need for further developments or improvements of a model [19]. In this paper, we present a systematic review and analysis of these models as presented in the literature.
- Related Works
- Coronaviruses are among the main pathogens that predominantly affect the human respiratory system. The focus of the literature review was, therefore, to outline the predominant variables and methodology used in studies related to the spread of the virus. People with prevalent illnesses such as diabetes, hypertension, diabetes, stroke, heart, or kidney failure, as well as elderly people with impaired immune systems, are at an increased risk of infection [20]. Closed areas with low ventilation and airflow may increase the risk of infection. The spread of the virus is believed to occur through respiratory droplets from coughing and sneezing, as with other respiratory viruses, including influenza virus and rhinoviruses. Aerosol transmission is also possible in case of protracted exposure to elevated aerosol concentrations in closed spaces [21].
- Several reports have defined a series of variables in terms of quarantine facilities, laboratory testing facilities, and healthcare capability, contributing to state preparedness to fight the pandemic. The most important and successful of these factors must be explored as an urgent solution to the pandemic. The availability of open data sets corresponding to different variables helps to accelerate studies and forge cooperation [22]. Environmental factors, such as pollution and basic sanitation, were considered in some studies. Several studies have also taken into consideration deaths due to COVID-19 and other demographic information [23,24]. Other studies and theories have pointed to comorbidities as a key factor in the number of COVID-19 cases [25,26]. Without considering comorbidities, fatalities may be mistakenly interpreted as exclusively COVID-19 deaths. Researchers from many universities in the USA have successfully predicted COVID-19 deaths. One such study was conducted at Columbia University and the CDC (2020), in which “death” was used as an exponential function and a social distance parameter prediction was made using a susceptible-exposed-infectious-removed (SEIR) meta-population model.
- Since the very beginning of the COVID-19 pandemic, numerous researchers have attempted to construct statistical models of the COVID-19 pandemic, as can be seen from a primary review of existing models. There are several differences in scope, assumptions, forecasts, the effects of interventions, and their impact on health services [27]. A PRISMA flow diagram based on the identification of studies from various databases, screening, and the eligibility and inclusion criteria is presented in Figure 4.
- SLR on COVID-19
- In the context of the COVID-19 pandemic, people across the world are using various methods to explore prediction models with the goal of addressing the problems caused by the pandemic. The motivation for this SLR was to help researchers across the world study the various prediction models that have been created by numerous authors from multiple countries by providing information on a comprehensive range of models in one place. A systematic review is a compilation of various studies related to a single topic. It aims to provide a comprehensive and unbiased review of all the relevant studies in a given field. Our SLR was conducted to determine which prediction models are currently available, and the objective of the study was to identify the various methods used to develop different types of prediction models and to conduct an effectiveness or quality assessment of the models, which helps to evaluate their accuracy. It is hoped that this SLR will help healthcare workers and researchers wisely and confidently choose accurate prediction models to facilitate healthcare management by arranging medical facilities and equipment. Researchers or scholars can enhance their research program by using this SLR to obtain up-to-date information on the various techniques used in prediction models, as well as their efficiency and accuracy. All currently available prediction models for COVID-19 were systematically reviewed and critically appraised. There are currently a number of diagnostic and prognostic models for COVID-19, all of which show moderate to excellent discrimination. To explore the different prediction models and find the best-suited model in terms of providing high accuracy while minimizing the burden on the healthcare system and improving care for patients, both the diagnosis and prognostic evaluation of diseases need to be improved. This study will influence decision-makers in various aspects.
- The selected papers deal with different techniques used to build predictive models for the spread of COVID-19. Various techniques are used for the modeling and to present results. Quantitative assessments were also evaluated based on the papers’ presentation of the percentage success/accuracy rate or error rates in statistical and regression models. This SLR sums up the research work of different prediction model developers in detail. In this SLR of prediction models related to the COVID-19 pandemic, we identified 30 studies with various prediction models. Among the 30 papers, the most cited ones were found to be those authored by Chinese researchers, followed by papers authored by Indian researchers and then papers authored by USA-based researchers (Table 4) [12,28–56].
- To identify the likelihood of future results based on historical data, predictive analytics uses data, statistical algorithms, and different techniques such as machine learning, autoregressive integrated moving average (ARIMA) models, SEIR models, and long short-term memory (LSTM) models. The present SLR also classified papers on the basis of the techniques used (Table 5) [12,28–56]. The most commonly used techniques used in predictive modeling and analysis were as follows:
- Machine learning is a technique used in which computers evaluate a data set and learn from the insights they gather. An artificial neural network is simulated by the use of complex algorithms that allow machines to classify, interpret, and understand data, and then use the insights that have been obtained to solve problems or make predictions. Common examples of machine learning include classification models, forecasts, medical diagnosis, image processing, regression, chatbots, and recommendation engines. Machine learning is a different branch of programming and is known to be an emerging technology.
- ARIMA models
- ARIMA models can be built in an array of software tools, including Python. These models are used in statistics and econometrics to measure events that happen over a span of time. ARIMA models predict future data in a series using past data. An ARIMA model can be constructed for any number series that display patterns and is not a random event series. For example, sales data from a footwear store would be an example of time series data because the data are collected over a period of time. One of the key characteristics is that the data are collected at constant, regular intervals [57].
- SEIR models
- SEIR models are commonly used for assessing infection data during the different phases of an infectious outbreak. SEIR models are among the most widely adopted mathematical frameworks to describe disease dynamics and forecast potential contagion scenarios. After an infectious disease outbreak, a SEIR model can be helpful in determining the efficacy of different interventions, such as lock-downs. These models are based on a series of complex ordinary differential equations that take into account the number of people who are sick, the pattern of people who recover over time after sickness, and the people who die [58].
- LSTM models
- LSTM models are a type of recurrent neural network (RNN) used to predict new infection numbers over time by processing and forecasting several issues related to time series. With repeating modules like an RNN, an LSTM model has a chain-like structure, except that instead of a single neural network layer as in RNNs, an LSTM model has 4 layers that communicate in a slightly different manner, each of which performs its own special network role. In an LSTM cell, each repeating module has a cell state. Through using various gates in the cell, the LSTM cell has the power to add or subtract information to the cell state. There are 3 gates for the standard LSTM cell that control the sum of data input or output to/from the cell state and protect the cell state.
- Regression models
- Regression analysis is a method of quantitative research that is used in studies modeling and analyzing several variables, where a dependent variable and 1 or more independent variables are included in the relationship. In basic terms, regression analysis is a mathematical approach used to evaluate the existence of the relationship between a dependent variable and 1 or more independent variables [59]. The 2 most widely used regression analyses are: (a) Logistic regression: in logistic regression, an independent variable is used to estimate the dependent variable. (b) Support vector regression (SVR): SVR provides the flexibility to determine how much error is suitable in a model and to find an appropriate line (or hyperplane in higher dimensions) to match the results.
- GLEM models
- Global epidemic and mobility (GLEM) models are being used in a number of COVID-19 related studies and analyses. These models involve a stochastic computational framework that combines high-resolution demographic and mobility data across the globe to predict the epidemic distribution across the globe. The goal of the GLEM model is to optimize versatility in specifying the disease compartment model and configuring the simulation scenario. It allows the user to set a number of criteria, including compartment-specific features, transition values, and environmental effects [60].
Related Literature
Machine learning
- This study identified the core literature on prediction models for COVID-19. The aim of this research was to review and analyze the articles in the literature related to prediction models for COVID-19. A prediction model is a method for predicting the future scenario based on present facts. This SLR was based on a manual search of 1,196 papers published from January to December 2020, out of which 30 documents were selected on the basis of inclusion and exclusion criteria. Our SLR was conducted to explore which prediction models are currently available, with the goals of identifying various methods used to develop different types of prediction models and to conduct an effectiveness or quality assessment of models, which helps in evaluating their accuracy.
- Based on this review, it is critical for statistical methods to be extensively used to predict the spread of infection. The LSTM [35] approach was used to track COVID-19 cases and to help government officials and policymakers in preparedness, with a root mean square error (RMSE) of 45.72. An ARIMA [47] model was used to predict the spread of COVID-19 infection with an average RMSE 44.81, followed by machine learning, artificial intelligence, and hybrid models. Lastly, in a few of the studies, mathematical modeling and network-based forecasting were used. SEIR models are among the most widely adopted mathematical frameworks to describe disease dynamics and forecast potential contagion scenarios. This SLR provides detailed information about various COVID-19 prediction models that can be adopted by researchers. This information can be used by healthcare professionals and by local government bodies in order to make decisions for managing healthcare facilities accordingly.
Conclusion
-
Ethics Approval
Not applicable.
-
Conflicts of Interest
The authors have no conflicts of interest to declare.
-
Funding
None.
-
Availability of Data
Data for literature review was taken from Google Scholar, Scopus, and Web of Science. All data generated or analysed during this study are included in this published article. For other data, these may be requested through the corresponding author.
-
Authors’ Contributions
Conception: all authors; Design: all authors; Supervision: RS, DRS; Literature review: SMS, NSK, PPM; Writing–original draft: all authors; Writing–review & editing: all authors.
Article information
Database's percentage share of COVID-19 cases reported as of January 2021.
This data is as of July 29, 2021 from Worldmeter (https://www.worldometers.info/coronavirus/).
| Database | Initial | Screened | Accepted |
|---|---|---|---|
| Google Scholar | 910 | 33 | 21 |
| Scopus | 210 | 19 | 4 |
| Web of Science | 76 | 10 | 5 |
| Total | 1,196 | 62 | 30 |
| Duplicates | 47 | 0 | 0 |
| Total selected | 1,149 | 62 | 30 |
| No. | Study | Objective | Type of model | Result | Quality assessment |
|---|---|---|---|---|---|
| 1 | Yang et al., 2020 [28] | To forecast COVID-19 patterns in China using a SEIR and AI model | SEIR model and AI model | · The model was effective in forecasting COVID-19 cases. | 95% CI |
| 2 | Liang et al., 2020 [29] | To forecast the risk of critical illness at hospital admission and identify survival of COVID-19 patients | Statistical software: LASSO, logistic regression model | · The score gives an estimation of the probability of critical disease progression for a hospitalized patient with COVID-19. | AUC (accuracy) was 0.88, 95% CI. |
| 3 | Yan et al., 2020 [30] | Relieving clinical burden and potentially reducing the mortality rate of COVID-19 | Machine learning tool: XGBoost | To predict patients with higher risk and potentially reduce mortality rate | Overall accuracy was 0.90 |
| · Survival prediction accuracy was 100%. | |||||
| · Mortality forecast accuracy was 81%. | |||||
| 4 | Gong et al., 2020 [31] | To predict the early detection of cases at high risk for progression to serious COVID-19 | Statistical analysis | · Results helped in COVID-19 patient identification for effective management. | Training cohort: |
| · AUC was 0.912, 95% CI. | |||||
| Validation cohort: | |||||
| · AUC was 0.853, 95% CI. | |||||
| 5 | Chatterjee et al., 2020 [32] | To develop a stochastic mathematical model to predict COVID-19 cases | SEIR | · To help in healthcare preparedness and in allocations of resources. | R0 was 2.28, growth rate of the epidemic in India was 1.15. |
| · The model suggested that herd immunity may be achieved when 55% to 65% of the population is infected. | |||||
| 6 | Hu et al., 2020 [12] | To predict confirmed COVID-19 cases and group cities into clusters according to transmission pattern | AI | · AI-based prediction showed significant accuracy and may act as a powerful tool for helping healthcare planning and policymaking. | Average errors: |
| • 6-Step (1.64%) | |||||
| • 7-Step (2.27%) | |||||
| • 8-Step (2.14%) | |||||
| • 9-Step (2.08%) | |||||
| • 10-Step (0.73%) | |||||
| 7 | Tomar & Gupta, 2020 [33] | To predict new COVID-19 cases using LSTM based techniques | LSTM | · Prediction corresponded to the original information with a reasonable CI. | ±5% CI |
| 8 | IHME COVID-19 Health Service Utilization Forecasting Team & Murray, 2020 [34] | To predict deaths and requirements of total beds for hospitals due to COVID-19 | Statistical model | · The model estimated that the number of COVID-19 deaths would range from 81,114 to 162,106 over the next 4 mo. | Not available. |
| 9 | Chimmula & Zhang, 2020 [35] | To track COVID-19 cases and to help government and policymakers prepare | LSTM, R0 method | · ARIMA | RMSE (45.70) |
| 10 | Pandey et al., 2020 [36] | To create a predictive model to assess the need for clinical treatment for patients | Machine learning models: SEIR, regression model | · Predictions will help check supply and medical assistance and help policymakers prepare. | RMSLE: |
| · SEIR model was 1.52. | |||||
| · regression model was 1.75. | |||||
| R0 between the 2 models was 2.02. | |||||
| 11 | Jehi et al., 2020 [37] | To develop a model for risk prediction for patients testing COVID-19 positive | Statistical prediction model: chi-square test | · Predictions could help direct healthcare preparedness. | C-statistic: |
| · Development cohort was 0.863. | |||||
| · Validation cohort was 0.840. | |||||
| 12 | Ardabili et al., 2020 [38] | To forecast the outbreak of COVID-19 using machine learning soft computing | Machine learning: logistic model. | Correlation coefficient | RMSE |
| · Italy (0.997) | · Italy (3358.1) | ||||
| · China (0.994) | · China (2524.44) | ||||
| · Iran (0.997) | · Iran (628.62) | ||||
| · USA (0.999) | · USA (350.33) | ||||
| · Germany (0.997) | · Germany (555.32) | ||||
| 13 | Sujath et al., 2020 [39] | To forecast COVID-19 pandemic using machine learning | Machine learning: LR, MLP | · 95% CI with LR and MLP | 95% CI |
| 14 | Qi et al., 2020 [40] | To predict the hospital stay of COVID-19 patients | Machine learning: logistic regression, RF | · Predictions exhibited feasibility and accuracy for hospital stay for patients with pneumonia associated with COVID-19 infection. | LR model: |
| · Sensitivity was 1.0. | |||||
| · Specificity was 0.89. | |||||
| RF model | |||||
| · Sensitivity was 0.75. | |||||
| · Specificity was 1.0. | |||||
| 15 | Ghosal et al., 2020 [41] | To forecast the number of deaths due to COVID-19 in India | Multiple regression and LR, auto-regression technique | · The estimated mortality rate (n) at the end of the 5th and 6th weeks was 211 and 467. | Multiple R was 0.9903. |
| R squared was 0.9807. | |||||
| Adjusted R squared was 0.9700. | |||||
| Standard error was 234.1358. | |||||
| 16 | Hoertel et al., 2020 [42] | To develop a prediction model to identify patients needing professional care | Statistical analysis: Kaplan-Meier method, R Foundation for statistical computing | · Cox model predicted with a high accuracy (p<0.05). | · AUC was 0.97. |
| · Overall C-statistic was 0.963 (95% CI, 0.936-0.99). | |||||
| 17 | Arora et al., 2020 [43] | To forecast the number of COVID-19 positive cases in 32 states and union territories of India using deep learning-based models | Deep learning: LSTM, RNN | · Model was highly accurate for short-term predictions (1–3 days) ahead. |
· MAPE range <3% · Weekly forecast 4%–8% |
| 18 | Salgotra et al., 2020 [44] | To forecast COVID-19 outbreaks in India and use time series study and model on CC and DC in 3 states of India, Maharashtra, Gujarat, and Delhi | GEP model | · The model was highly effective in forecasting both reported cases and deaths around India. | · Lowest R value: 0.9881, DC in Delhi, |
| · highest value was 0.9999, RC in India | |||||
| 19 | Dutta and Bandyopadhyay, 2020 [45] | To validate the predicted outcome of COVID-19 cases using machine learning | LSTM, GRU | Accuracy level | RMSE |
| · Confirmed cases: 87% | · Confirmed cases: 30.15% | ||||
| · Negative cases: 67.8% | · Negative cases: 49.4% | ||||
| · Deceased cases: 62% | · Deceased cases: 4.16% | ||||
| · Released cases: 40.5% | · Released cases: 13.72% | ||||
| 20 | Zhao et al., 2020 [46] | To develop risk ratings based on clinical categories and to forecast COVID-19 ICU admission and mortality | Logistic regression: multivariable regression model | · Predictions will significantly assist the flow of COVID-19 patients and distribute resources accordingly. | · ICU admission: AUC was 0.74, 95% CI. |
| · Predicting mortality: AUC was 0.82, 95% CI. | |||||
| 21 | Hernandez-Matamoros et al., 2020 [47] | To predict COVID-19 behaviors in order to make future plans and hence to forecast the progress of the virus | ARIMA | · The model was able to predict the behavior of spread of COVID-19 infection. | RMSE average of 144.81. |
| 22 | Alazab et al., 2020 [48] | To predict COVID-19 cases across the world using an AI-based technique | PA, ARIMA, LSTM | · PA delivered the best performance. | Accuracy: |
| · The model predicted COVID-19 cases and achieved an F-measure of 99%. | · Australia was 94.80%. | ||||
| · Jordan was 88.43%. | |||||
| 23 | Parbat and Chakraborty, 2020 [49] | To predict the total number of deaths, recovered cases, cumulative number of confirmed cases, and number of daily cases | Vector regression model | The model: | RMSE: |
| · Functioned well in fitting the total cases | · Total deaths: 0.092142 | ||||
| · Poor fit for the daily number of cases | · Total recovered: 0.174036 | ||||
| · Daily confirmed: 0.330830 | |||||
| · Daily deaths: 0.361727 | |||||
| 24 | Zhao et al., 2020 [50] | To predict COVID-19 confirmed cases using 6 rolling grey Verhulst models | Rolling Grey Verhulst model | · Predictions exhibited good accuracy. | MAPE: training stage |
| · Six models predicted S-shaped change characteristics consistently. | · Max (4.74%) | ||||
| · Min (1.80%) | |||||
| Testing stage | |||||
| · Max (4.72%) | |||||
| · Min (1.65%) | |||||
| 25 | Achterberg et al., 2020 [51] | To evaluate a diverse range of forecast algorithms for COVID-19 | Network-based forecasting | · The algorithm performed well in predicting COVID-19 cases and was superior to any other prediction algorithm. | NIPA |
| · Hubei was 0.122. | |||||
| · The Netherlands was 0.038. | |||||
| 26 | Fernandez et al., 2021 [52] | To develop a forecasting algorithm to consider patient survival | Logistic regression: multivariate logistic regression | · Patients that would be able to survive were classified by age, CRP, platelet count, and number of lung consolidations. | AUC was 0.8129. |
| GOF: Hosmer and Lemeshow test, p=0.018; 95% CI (0.773–0.853, p<0.001) | |||||
| 27 | Li et al., 2020 [53] | To develop a prediction model for identifying patients at an increased risk of COVID-19 death | Machine learning: autoencoder model, logistic regression, SVM, RF | · The model exhibited specificity and accuracy above 0.9. | Logistic regression, SVM, RF |
| · Sensitivities below 0.4. | |||||
| · Autoencoder scores above a sensitivity value of 0.4. | |||||
| 28 | Siwiak et al., 2020 [54] | To develop a global model for COVID-19 in terms of the number of infected cases | GLEAM | · Presented a percentage difference over time between the number of reported, confirmed cases and CI limits for different modeled predictions. | 95% CI |
| 29 | Bhandari et al., 2020 [55] | To predict the progression of COVID-19 in India using ARIMA | ARIMA | · The COVID-19 forecast helps the government and policy makers to optimize resources and make decisions. | 95% CI |
| 30 | Muhammad et al., 2021 [56] | To forecast COVID-19 infection using machine learning | Machine learning: logistic regression, decision tree, support vector machine, naive Bayes, and artificial neutral network | · Decision tree model accuracy was 94.99%. | RMSE: LMST (27.187) |
| · Support vector machine model sensitivity was 93.34%. | LR (7.562) | ||||
| · Naive Bayes model has a specificity of 94.30%. |
COVID-19, coronavirus disease 2019; SEIR, susceptible-exposed-infectious-removed; AI, artificial intelligence; CI, confidence interval; LASSO, least absolute shrinkage and selection operator; AUC, area under the curve; XGBoost, eXtreme gradient boosting; LSTM, long short-term memory; ARIMA, autoregressive integrated moving average; RMSE, root mean square error; RMSLE, root mean square logarithmic error; LR, linear regression; MLP, multilayer perceptron; RF, random forest; RNN, recurrent neural network; MAPE, mean absolute percentage error; CC, confirmed case; DC, death case; GEP, genetic evolutionary programming; RC, reported case; GRU, gated recurrent unit; ICU, intensive care unit; PA, prophet algorithm; NIPA, network inference-based prediction algorithm; CRP, C-reactive protein; GOF, goodness of fit; SVM, support vector machine; GLEAM, global epidemic and mobility framework.
| No. | Study | Year | Country | Citation (January 2, 2021) | Model |
|---|---|---|---|---|---|
| 1 | Yang et al. [28] | 2020 | China | 467 | SEIR and AI model |
| 2 | Liang et al. [29] | 2020 | China | 327 | Statistical software |
| 3 | Yan et al. [30] | 2020 | China | 194 | Machine learning |
| 4 | Gong et al. [31] | 2020 | China | 134 | Statistical analysis |
| 5 | Chatterjee et al. [32] | 2020 | India | 131 | SEIR |
| 6 | Hu et al. [12] | 2020 | China | 130 | Artificial intelligence |
| 7 | Tomar & Gupta [33] | 2020 | India | 129 | LSTM |
| 8 | IHME COVID-19 Health Service Utilization Forecasting Team & Murray [34] | 2020 | USA | 119 | Statistical model |
| 9 | Chimmula & Zhang [35] | 2020 | Canada | 99 | LSTM |
| 10 | Pandey et al. [36] | 2020 | India | 57 | Machine learning |
| 11 | Jehi et al. [37] | 2020 | USA | 45 | Statistical analysis |
| 12 | Ardabili et al. [38] | 2020 | Worldwide scenario | 41 | Machine learning |
| 13 | Sujath et al. [39] | 2020 | India | 41 | Machine learning |
| 14 | Qi et al. [40] | 2020 | Worldwide scenario | 41 | Machine learning |
| 15 | Ghosal et al. [41] | 2020 | India | 39 | Regression model |
| 16 | Hoertel et al. [42] | 2020 | France | 37 | Statistical analysis |
| 17 | Arora et al. [43] | 2020 | India | 34 | LSTM, RNN |
| 18 | Salgotra et al. [44] | 2020 | India | 34 | GEP model |
| 19 | Dutta & Bandyopadhyay [45] | 2020 | India | 33 | LSTM, GRU |
| 20 | Zhao et al. [46] | 2020 | China | 13 | Logistic regression |
| 21 | Hernandez-Matamoros et al. [47] | 2020 | Chile | 11 | ARIMA |
| 22 | Alazab et al. [48] | 2020 | Jordon | 9 | PA, ARIMA, LSTM |
| 23 | Parbat & Chakraborty [49] | 2020 | India | 9 | Regression model |
| 24 | Zhao et al. [50] | 2020 | China | 6 | Grey Verhulst |
| 25 | Achterberg et al. [51] | 2020 | China | 2 | Network-based forecasting |
| 26 | Fernandez et al. [52] | 2021 | UK | 2 | AI |
| 27 | Li et al. [53] | 2020 | Worldwide scenario | 1 | GLEM |
| 28 | Siwiak et al. [54] | 2020 | India | 1 | ARIMA |
| 29 | Bhandari et al. [55] | 2020 | UK | - | Logistic regression |
| 30 | Muhammad et al. [56] | 2021 | Mexico | - | Machine learning |
SEIR, susceptible-exposed-infectious-removed; AI, artificial intelligence; LSTM, long short-term memory; RNN, recurrent neural network; GEP, genetic evolutionary programming; GRU, gated recurrent unit; ARIMA, autoregressive integrated moving average; PA, prophet algorithm; GLEM, global epidemic and mobility.
- 1. Bohmer R, Pisano G, Sadun R, et al. How hospitals can manage supply shortages as demand surges [Internet]. Harvard Business Review; 2020 Apr 3 ; [cited 2020 April 11]. Available from: https://hbr.org/2020/04/how-hospitals-can-manage-supply-shortages-as-demand-surges?.
- 2. Alamoodi AH, Zaidan BB, Zaidan AA, et al. Sentiment analysis and its applications in fighting COVID-19 and infectious diseases: a systematic review. Expert Syst Appl 2021;167:114155. ArticlePubMed
- 3. Albahri OS, Zaidan AA, Albahri AS, et al. Systematic review of artificial intelligence techniques in the detection and classification of COVID-19 medical images in terms of evaluation and benchmarking: taxonomy analysis, challenges, future solutions and methodological aspects. J Infect Public Health 2020;13:1381−96.ArticlePubMedPMC
- 4. Albahri AS, Al-Obaidi JR, Zaidan AA, et al. Multi-biological laboratory examination framework for the prioritization of patients with COVID-19 based on integrated AHP and group VIKOR methods. Int J Inf Technol Decis Mak 2020;19:1247−69.Article
- 5. Albahri AS, Hamid RA, Albahri OS, et al. Detection-based prioritisation: framework of multi-laboratory characteristics for asymptomatic COVID-19 carriers based on integrated Entropy-TOPSIS methods. Artif Intell Med 2021;111:101983. ArticlePubMed
- 6. Albahri OS, Al-Obaidi JR, Zaidan AA, et al. Helping doctors hasten COVID-19 treatment: towards a rescue framework for the transfusion of best convalescent plasma to the most critical patients based on biological requirements via ml and novel MCDM methods. Comput Methods Programs Biomed 2020;196:105617. ArticlePubMedPMC
- 7. Suri JC, Sen MK. Pandemic influenza-Indian experience. Lung India 2011;28:2−4.ArticlePubMedPMC
- 8. Regmi K, Lwin CM. Impact of social distancing measures for preventing coronavirus disease 2019 [COVID-19]: a systematic review and meta-analysis protocol [Preprint]. Posted 2020 Jun 16. medRxiv 2020.06.13.20130294. https://doi.org/10.1101/2020.06.13.20130294.Article
- 9. Hui DS, I Azhar E, Madani TA, et al. The continuing 2019-nCoV epidemic threat of novel coronaviruses to global health: the latest 2019 novel coronavirus outbreak in Wuhan, China. Int J Infect Dis 2020;91:264−6.ArticlePubMedPMC
- 10. Ghinai I, McPherson TD, Hunter JC, et al. First known person-to-person transmission of severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) in the USA. Lancet 2020;395:1137−44.PubMedPMC
- 11. Saraswathi S, Mukhopadhyay A, Shah H, et al. Social network analysis of COVID-19 transmission in Karnataka, India. Epidemiol Infect 2020;148:e230.ArticlePubMed
- 12. Hu Z, Ge Q, Li S, et al. Artificial intelligence forecasting of covid-19 in China [Preprint]. Posted 2020 Mar 1. arXiv:2002.07112. https://arxiv.org/abs/2002.07112.
- 13. Decaro N, Lorusso A. Novel human coronavirus (SARS-CoV-2): a lesson from animal coronaviruses. Vet Microbiol 2020;244:108693. ArticlePubMedPMC
- 14. World Health Organization (WHO). Coronavirus disease 2019 (COVID-19): situation report, 35. Geneva: WHO; 2020.
- 15. Okoli C. A guide to conducting a standalone systematic literature review. Commun Assoc Inf Syst 2015;37:43https://doi.org/10.17705/1CAIS.03743.Article
- 16. Tranfield D, Denyer D, Smart P. Towards a methodology for developing evidence-informed management knowledge by means of systematic review. Br J Manag 2003;14:207−22.Article
- 17. Moher D, Liberati A, Tetzlaff J, et al. Reprint--preferred reporting items for systematic reviews and meta-analyses (PRISMA): the PRISMA statement. Phys Ther 2009;89:873−80.ArticlePubMed
- 18. Geisser S. Predictive inference: an introduction. New York: Chapman & Hall; 1993.
- 19. Allotey J, Snell KI, Chan C, et al. External validation, update and development of prediction models for pre-eclampsia using an Individual Participant Data (IPD) meta-analysis: the International Prediction of Pregnancy Complication Network (IPPIC pre-eclampsia) protocol. Diagn Progn Res 2017;1:16. ArticlePubMedPMC
- 20. Raghupathi V, Ren J, Raghupathi W. Studying public perception about vaccination: a sentiment analysis of tweets. Int J Environ Res Public Health 2020;17:3464. ArticlePubMedPMC
- 21. Epidemiology Working Group for NCIP Epidemic Response, Chinese Center for Disease Control and Prevention. [The epidemiological characteristics of an outbreak of 2019 novel coronavirus diseases (COVID-19) in China]. Zhonghua Liu Xing Bing Xue Za Zhi 2020;41:145−51. Chinese.PubMed
- 22. Schwalbe N. We could be vastly overestimating the death rate for COVID-19. Here's why. World Economic Forum; 2020 Apr 4 [cited 2020 Aug 2]. Available from: https://www.weforum.org/agenda/2020/04/we-could-be-vastly-overestimating-the-death-rate-for-covid-19-heres-why/.
- 23. Soyiri IN, Reidpath DD. An overview of health forecasting. Environ Health Prev Med 2013;18:1−9.ArticlePubMed
- 24. Zeegers MP, Bours MJ, Freeman MD. Methods used in forensic epidemiologic analysis. Edited by Freeman MD, Zeegers MP: Forensic epidemiology: principles and practice. Cambridge: Academic Press; 2016. pp 71−110.
- 25. Guan WJ, Liang WH, Zhao Y, et al. Comorbidity and its impact on 1590 patients with COVID-19 in China: a nationwide analysis. Eur Respir J 2020;55:2000547. ArticlePubMedPMC
- 26. Wang B, Li R, Lu Z, et al. Does comorbidity increase the risk of patients with COVID-19: evidence from meta-analysis. Aging (Albany NY) 2020;12:6049−57.ArticlePubMedPMC
- 27. Kotwal A, Yadav AK, Yadav J, et al. Predictive models of COVID-19 in India: a rapid review. Med J Armed Forces India 2020;76:377−86.ArticlePubMedPMC
- 28. Yang Z, Zeng Z, Wang K, et al. Modified SEIR and AI prediction of the epidemics trend of COVID-19 in China under public health interventions. J Thorac Dis 2020;12:165−74.ArticlePubMedPMC
- 29. Liang W, Liang H, Ou L, et al. Development and validation of a clinical risk score to predict the occurrence of critical illness in hospitalized patients with COVID-19. JAMA Intern Med 2020;180:1081−9.ArticlePubMed
- 30. Yan L, Zhang HT, Goncalves J, et al. An interpretable mortality prediction model for COVID-19 patients. Nat Mach Intell 2020;2:283−8.ArticlePDF
- 31. Gong J, Ou J, Qiu X, et al. A tool for early prediction of severe coronavirus disease 2019 (COVID-19): a multicenter study using the risk nomogram in Wuhan and Guangdong, China. Clin Infect Dis 2020;71:833−40.ArticlePubMed
- 32. Chatterjee K, Chatterjee K, Kumar A, et al. Healthcare impact of COVID-19 epidemic in India: a stochastic mathematical model. Med J Armed Forces India 2020;76:147−55.ArticlePubMedPMC
- 33. Tomar A, Gupta N. Prediction for the spread of COVID-19 in India and effectiveness of preventive measures. Sci Total Environ 2020;728:138762. ArticlePubMedPMC
- 34. IHME COVID-19 Health Service Utilization Forecasting Team, Murray CJ. Forecasting COVID-19 impact on hospital bed-days, ICU-days, ventilator-days and deaths by US state in the next 4 months [Preprint]. Posted 2020 Mar 30. medRxiv 2020.03.27.20043752. https://doi.org/10.1101/2020.03.27.20043752.Article
- 35. Chimmula VK, Zhang L. Time series forecasting of COVID-19 transmission in Canada using LSTM networks. Chaos Solitons Fractals 2020;135:109864. ArticlePubMedPMC
- 36. Pandey G, Chaudhary P, Gupta R, et al. SEIR and Regression Model based COVID-19 outbreak predictions in India [Preprint]. Posted 2020 Apr 1. arXiv:2004.00958. https://arxiv.org/abs/2004.00958.Article
- 37. Jehi L, Ji X, Milinovich A, et al. Individualizing risk prediction for positive coronavirus disease 2019 testing: results from 11,672 patients. Chest 2020;158:1364−75.ArticlePubMedPMC
- 38. Ardabili SF, Mosavi A, Ghamisi P, et al. COVID-19 outbreak prediction with machine learning. Algorithms 2020;13:249. Article
- 39. Sujath R, Chatterjee JM, Hassanien AE. A machine learning forecasting model for COVID-19 pandemic in India. Stoch Environ Res Risk Assess 2020;34:959−72.ArticlePubMedPMC
- 40. Qi X, Jiang Z, Yu Q, et al. Machine learning-based CT radiomics model for predicting hospital stay in patients with pneumonia associated with SARS-CoV-2 infection: a multicenter study [Preprint]. Posted 2020 Mar 3. medRxiv 2020.02.29.20029603. https://doi.org/10.1101/2020.02.29.20029603.Article
- 41. Ghosal S, Sengupta S, Majumder M, et al. Linear Regression Analysis to predict the number of deaths in India due to SARS-CoV-2 at 6 weeks from day 0 (100 cases - March 14th 2020). Diabetes Metab Syndr 2020;14:311−5.ArticlePubMedPMC
- 42. Hoertel N, Blachier M, Blanco C, et al. A stochastic agent-based model of the SARS-CoV-2 epidemic in France. Nat Med 2020;26:1417−21.ArticlePubMed
- 43. Arora P, Kumar H, Panigrahi BK. Prediction and analysis of COVID-19 positive cases using deep learning models: a descriptive case study of India. Chaos Solitons Fractals 2020;139:110017. ArticlePubMedPMC
- 44. Salgotra R, Gandomi M, Gandomi AH. Evolutionary modelling of the COVID-19 pandemic in fifteen most affected countries. Chaos Solitons Fractals 2020;140:110118. ArticlePubMedPMC
- 45. Dutta S, Bandyopadhyay SK. Machine learning approach for confirmation of COVID-19 cases: positive, negative, death and release [Preprint]. Posted 2020 Mar 30. medRxiv 2020.03.25.20043505. https://doi.org/10.1101/2020.03.25.20043505.Article
- 46. Zhao Z, Chen A, Hou W, et al. Prediction model and risk scores of ICU admission and mortality in COVID-19. PLoS One 2020;15:e0236618.ArticlePubMedPMC
- 47. Hernandez-Matamoros A, Fujita H, Hayashi T, et al. Forecasting of COVID19 per regions using ARIMA models and polynomial functions. Appl Soft Comput 2020;96:106610. ArticlePubMedPMC
- 48. Alazab M, Awajan A, Mesleh A, et al. COVID-19 prediction and detection using deep learning. Int J Comput Inf Syst Ind Manag Appl 2020;12:168−81.
- 49. Parbat D, Chakraborty M. A python based support vector regression model for prediction of COVID19 cases in India. Chaos Solitons Fractals 2020;138:109942. ArticlePubMedPMC
- 50. Zhao YF, Shou MH, Wang ZX. Prediction of the number of patients infected with COVID-19 based on rolling grey Verhulst models. Int J Environ Res Public Health 2020;17:4582. ArticlePubMedPMC
- 51. Achterberg MA, Prasse B, Ma L, et al. Comparing the accuracy of several network-based COVID-19 prediction algorithms. Int J Forecast 2020;Oct 9 [Epub]. https://doi.org/10.1016/j.ijforecast.2020.10.001.Article
- 52. Fernandez A, Obiechina N, Koh J, et al. Survival prediction algorithms for COVID-19 patients admitted to a UK district general hospital. Int J Clin Pract 2021;75:e13974.ArticlePubMed
- 53. Li Y, Horowitz MA, Liu J, et al. Individual-level fatality prediction of COVID-19 patients using AI methods. Front Public Health 2020;8:587937. ArticlePubMedPMC
- 54. Siwiak M, Szczesny P, Siwiak M. From the index case to global spread: the global mobility based modelling of the COVID-19 pandemic implies higher infection rate and lower detection ratio than current estimates. PeerJ 2020;8:e9548.ArticlePubMedPMC
- 55. Bhandari S, Tak A, Gupta J, et al. Evolving trajectories of COVID-19 curves in India: prediction using autoregressive integrated moving average modeling [Preprint]. Posted 2020 Jul 7. Research Square. c.Article
- 56. Muhammad LJ, Algehyne EA, Usman SS, et al. Supervised machine learning models for prediction of COVID-19 infection using epidemiology dataset. SN Comput Sci 2021;2:11. ArticlePubMed
- 57. Brownlee J. Introduction to time series forecasting with Python: how to prepare data and develop models to predict the future. San Juan (PR): Machine Learning Mastery; 2017.
- 58. Parham PE, Michael E. Outbreak properties of epidemic models: the roles of temporal forcing and stochasticity on pathogen invasion dynamics. J Theor Biol 2011;271:1−9.ArticlePubMed
- 59. Ray S. 7 Regression Techniques you should know [Internet]. Indore: Analytics Vidhya; 2015 Aug 14 [cited 2020 Aug 2]. Available from: https://www.analyticsvidhya.com/blog/2015/08/comprehensive-guide-regression/.
- 60. Van den Broeck W, Gioannini C, et al. The GLEaMviz computational tool, a publicly available software to explore realistic epidemic spreading scenarios at the global scale. BMC Infect Dis 2011;11:37. ArticlePubMedPMC
References
Figure & Data
References
Citations

- The Telemedicine Demand Index and its Utility in Managing COVID-19 Case Surges
Martin Yong Kwong Lee, Kie Beng Goh, Deanna Xiuting Koh, Si Jack Chong, Raymond Swee Boon Chua
Telemedicine and e-Health.2024; 30(2): 545. CrossRef - Vaccination compartmental epidemiological models for the delta and omicron SARS-CoV-2 variants
J. Cuevas-Maraver, P.G. Kevrekidis, Q.Y. Chen, G.A. Kevrekidis, Y. Drossinos
Mathematical Biosciences.2024; 367: 109109. CrossRef - The reporting completeness and transparency of systematic reviews of prognostic prediction models for COVID-19 was poor: a methodological overview of systematic reviews
Persefoni Talimtzi, Antonios Ntolkeras, Georgios Kostopoulos, Konstantinos I. Bougioukas, Eirini Pagkalidou, Andreas Ouranidis, Athanasia Pataka, Anna-Bettina Haidich
Journal of Clinical Epidemiology.2024; 167: 111264. CrossRef - A comprehensive benchmark for COVID-19 predictive modeling using electronic health records in intensive care
Junyi Gao, Yinghao Zhu, Wenqing Wang, Zixiang Wang, Guiying Dong, Wen Tang, Hao Wang, Yasha Wang, Ewen M. Harrison, Liantao Ma
Patterns.2024; 5(4): 100951. CrossRef - A study of learning models for COVID-19 disease prediction
Sakshi Jain, Pradeep Kumar Roy
Journal of Ambient Intelligence and Humanized Comp.2024; 15(4): 2581. CrossRef - Is It Possible to Predict COVID-19? Stochastic System Dynamic Model of Infection Spread in Kazakhstan
Berik Koichubekov, Aliya Takuadina, Ilya Korshukov, Anar Turmukhambetova, Marina Sorokina
Healthcare.2023; 11(5): 752. CrossRef - Early triage echocardiography to predict outcomes in patients admitted with COVID‐19: a multicenter study
Daniel Peck, Andrea Beaton, Maria Carmo Nunes, Nicholas Ollberding, Allison Hays, Pranoti Hiremath, Federico Asch, Nitin Malik, Christopher Fung, Craig Sable, Bruno Nascimento
Echocardiography.2023; 40(5): 388. CrossRef - Static Seeding and Clustering of LSTM Embeddings to Learn From Loosely Time-Decoupled Events
Christian G. Manasseh, Razvan Veliche, Jared Bennett, Hamilton Scott Clouse
IEEE Access.2023; 11: 64219. CrossRef - Harnessing the power of AI: Advanced deep learning models optimization for accurate SARS-CoV-2 forecasting
Muhammad Usman Tariq, Shuhaida Binti Ismail, Muhammad Babar, Ashir Ahmad, Lin Wang
PLOS ONE.2023; 18(7): e0287755. CrossRef - Development and validation of COEWS (COVID-19 Early Warning Score) for hospitalized COVID-19 with laboratory features: A multicontinental retrospective study
Riku Klén, Ivan A Huespe, Felipe Aníbal Gregalio, Antonio Lalueza Lalueza Blanco, Miguel Pedrera Jimenez, Noelia Garcia Barrio, Pascual Ruben Valdez, Matias A Mirofsky, Bruno Boietti, Ricardo Gómez-Huelgas, José Manuel Casas-Rojo, Juan Miguel Antón-Santos
eLife.2023;[Epub] CrossRef - Dynamic transmission modeling of COVID-19 to support decision-making in Brazil: A scoping review in the pre-vaccine era
Gabriel Berg de Almeida, Lorena Mendes Simon, Ângela Maria Bagattini, Michelle Quarti Machado da Rosa, Marcelo Eduardo Borges, José Alexandre Felizola Diniz Filho, Ricardo de Souza Kuchenbecker, Roberto André Kraenkel, Cláudia Pio Ferreira, Suzi Alves Cam
PLOS Global Public Health.2023; 3(12): e0002679. CrossRef - Predictive Models for Forecasting Public Health Scenarios: Practical Experiences Applied during the First Wave of the COVID-19 Pandemic
Jose M. Martin-Moreno, Antoni Alegre-Martinez, Victor Martin-Gorgojo, Jose Luis Alfonso-Sanchez, Ferran Torres, Vicente Pallares-Carratala
International Journal of Environmental Research an.2022; 19(9): 5546. CrossRef - Artificial intelligence and clinical deterioration
James Malycha, Stephen Bacchi, Oliver Redfern
Current Opinion in Critical Care.2022; 28(3): 315. CrossRef


 PubReader
PubReader ePub Link
ePub Link Cite
Cite